Projektdokumentation Künstliche Intelligenz
Inhalt
Idee
Die zugrundeliegende Idee des Projektes ist ein handschriftlicher Taschenrechner, der mithilfe von Methoden und Konzepten des maschinellen Lernens die gezeichneten Zahlen und mathematischen Operatoren klassifziert. Durch das Erkennen der einzelnen Zeichen ist es möglich, Rechnungen durchzuführen und das Ergebnis dem Nutzer der Applikation zu präsentieren.
Daten
Als Datengrundlage wurde das Handwritten Dataset von Kaggle verwendet.
Das Datenset bietet über 300.000 Beispielbilder für insgesamt 82 unterschiedliche Symbole und Zahlen. Die Bilder im Datenset sind RGB Bilder mit der Auflösung $45 \times 45$ Pixeln.
Drei Beispielbilder des Datensets für “4”,”+” und “6” sind im folgenden illustriert.
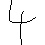
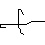
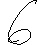
Im Rahmen des Projektes wurde sich jedoch auf 14 der 82 unterschiedlichen Klassen beschränkt, sodass der Rechner auf die Erkennung der Grundrechenarten und arabischen Ziffern limitiert ist:
Insgesamt sind für die ausgewählten Klassen 157.485 Beispielbilder vorhanden. Diese sind durch die Ordnerstruktur des Datensets bereits in verschiedene Ordner für Beispiele der jeweiligen Klassen eingeteilt.
Die nachfolgende Grafik zeigt die Anzahl der Daten pro Klasse, die für das Training und das Testen der ausgewählten Algorithmen verwendet wurden.
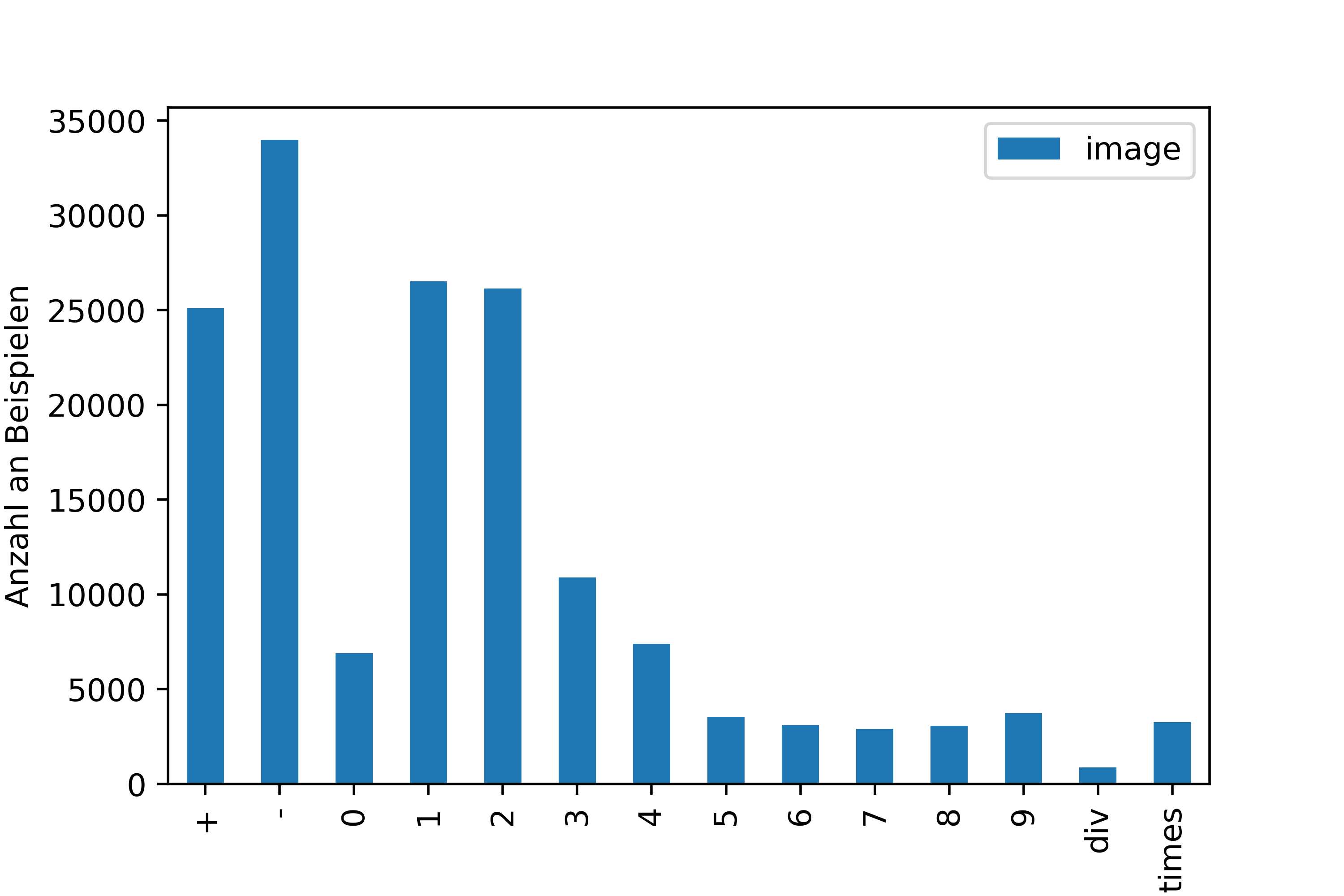
Genaue Verteilung der Beispieldaten pro Zeichen:
| Zeichen | + | - | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | div | times |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl Daten | 25.112 | 33.997 | 6.914 | 26.520 | 26.141 | 10.909 | 7.396 | 3.545 | 3.118 | 2.909 | 3.068 | 3.737 | 868 | 3.251 |
Für das Training und den Test wurde eine Einteilung der Daten in 80% Trainings- und 20% Testdaten verwendet. Dementsprechend wurden insgesamt für das Training 125.988 und für die Tests 31.497 Beispieldaten verwendet.
Zunächst wurde vermutet, dass durch die ungleiche Verteilung der Klassen Probleme auftreten würden und deshalb verschiedene Optionen, vorallem zum Hinzufügen von weiteren Beispielen der Klassen, die sehr wenige Beispielbilder in Relation zu den anderen Klassen aufweisen, in Betracht gezogen wurden. Exemplarisch sei hier die Anzahl an Beispielen der Klasse “$div$ $(\div)$” zu nennen. Mit nur 868 Beispielbilder liegen dieser Klasse vergleichsweise sehr wenige Daten vor.
Schnell wurde die starke Limitierung weiterer Datensets festgestellt, weswegen letztlich keine Änderungen an den Daten des Projektes durchgeführt wurden.
Preprocessing
Da alle Daten zunächst als Bilddateien (.jpg) vorliegen und nur durch die gegebene Ordnerstruktur den Klassen zuzuordnen sind, müssen diese in eine Matrix von Farbwerten konvertiert und entsprechend gelabelt werden. Da jedes Bild zunächst die Größe $45 \times 45$ besitzt, wird für jedes Bild (RGB) eine Matrix $M$ generiert, die die Pixelwerte der jeweiligen Farben des Kanals repräsentiert:
Für das Preprocessing werden unterschiedliche Schritte für jedes Bild durchlaufen. Im vorliegenden Fall ist beispielsweise eine RGB Farbkodierung nicht notwendig, da die Farben der handschriftlichen Eingaben eine unwesentliche Eigenschaft darstellen. Aufgrund dessen wurde entschieden, dass alle Daten an Stelle von RGB, schwarz-weiß kodiert sind (8-Bit Graustufen). Somit hat Jede Pixelmatrix $M$ eines Eingabebildes nun die Form:
Im Laufe des Projektes hat sich herausgestellt, dass die Trainingsdaten alle eng geschnitten sind und mindestens an einer Kante des Bildrahmens anliegen. Um sicherzustellen, dass dies auch für neue, ungesehen Handschriftbilder gegeben ist, wird möglichst viel vom umliegenden Rand abgeschnitten, ohne das Verhältnis des Bildes zu manipulieren.
Da so gut wie alle Trainingsdaten die besagte Größe von $45 \times 45$ besitzen, waren auch hier Überlegungen notwendig, um die Eingaben für den Benutzer des Taschenrechners nicht auf diese Größe zu beschränken. Aus diesem Grund werden alle gezeichneten Symbole, unabhängig ihrer Größe, auf eine Bildgröße von 45x45 skaliert. Diese dienen dann als Grundlage für den weiteren Prozess, um auf diesen Daten geeignete Algorithmen anzuwenden.
Folgendes Beispiel zeigt die Preprocessing-Schritte:
- Eingabebild für die Klasse “2” der Größe $500 \times 850$. Sollte das Bild noch nicht in schwarz-weiß vorliegen, so würde es konvertiert werden.
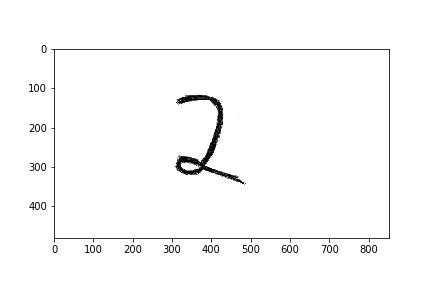
- Das Bild wird entsprechend zugeschnitte, sodass es möglichst auf den eigentlichen Inhalt beschränkt wird.
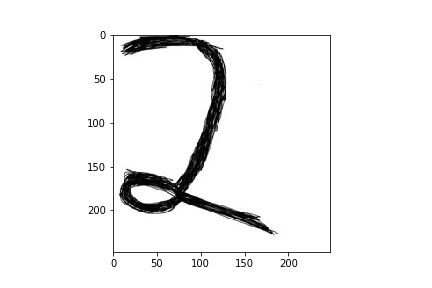
- Der letzte Schritt ist das Konvertieren des bereits bearbeiteten Bildes auf die gewählte Standardgröße $45 \times 45$.
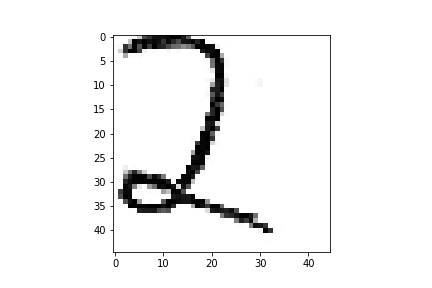
- Im Anschluss kann das Bild verwendet werden, um eine Matrix $M$ der Graustufenwerte zu verwenden, wobei der Wert $0 \rightarrow \text{schwarz}$ und der Wert $255 \rightarrow \text{weiß}$ entspricht.
- Um nun die Matrix zu nutzen und einen Featurevektor als Eingabe für diverse Klassifikationsalgortihmen zu verwenden, werden alle Zeilenvektoren transponiert und aneinandergehangen, sodass ein Vektor $\vec{v} \in \mathbb{R}^{2054}$ entsteht (Flattening).
Dieser dient nun als Eingabe der ausgewählten Algorithmen.
Für die Trainingsdaten wurde ein ähnlicher Prozess durchlaufen. Diese werden dann anschließend, zusammen mit dem passenden Label, abgespeichert, sodass die Preprocessing-Schritte für zukünftige Trainings ausgelassen werden können. Die Datenstruktur hat somit folgende Form:
Algorithmen
Aus technischer Sicht liegt ein Klassifizierungsproblem mit 14 verschiedenen Klassen vor. Es gilt also ein Modell (Hypothesenfunktion) zu finden, welches durch Eingabe von handschriftlichen Bildern in Form einer $45\times45$ Matrix eine geeignete Klasse findet.
Zur Lösung des Problems der Klassifzierung wurden zunächst gängige und einfach zu trainierende Algorithmen ausgewählt. Da alle vorliegenden Daten inklusive deren Klassen-Label vorliegen und verwendet werden können, werden hier vorallem Algorithmen des überwachten Lernens genutzt.
Random Forest / Naive Bayes
Zunächst wurden einfache Algortihmen wie der Naive Bayes, der auf der bedingten Wahrscheinlichkeitsberechnung und dem Satz von Bayes basiert, betrachtet. Durch schlechte Trainingsergebnisse wurde die Nutzung dieses Algorithmus jedoch verworfen.
Zusätzlich wurde ein Random Forest Klassifikator getestet, der zwar sehr gute Testergebnisse lieferte (Accuracy = 0.99) jedoch in der Generalisierung durch ungesehene, gemalte Beispiele sehr schlecht war und die Klassifizierung womöglich durch eine Überangepasstheit des Modells gelitten hat.
Diese Erkenntnisse unterstüzen weiter die Aussage, dass diese vergleichweise “einfachen” Algorithmen zur Klassifizierung von Bildern eher ungeeignet sind.
Im nächsten Schritt werden die etwas populäreren Algorithmen die im Bereich des maschinellen Sehens häufig Anwendung finden, betrachtet.
Support Vector Machine (SVC)
Die Support Vector Machine, speziell der Support Vector Classifier (SVC) wurde als weitere Alternative zur Klassifizierung der handschriftlichen Zahlen und Symbolen verwendet.
Der SVC ist ein sogennanter “large margin”-Klassifikator, da versucht wird eine Trenngeraden zwischen die Beispiele einer Klasse zu konstruieren. Dabei wird versucht, eine maximale “margin”, also einen maximalen Abstand zwischen den Grenzbeispielen (den sogenannten Support Vectors) einer jeden Klasse zu erreichen.
Im vorliegenden Fall wurde sich für einen SVC mit linearem Kernel und nach verschiedenen Experimenten einen Parameterwert für $C = 1$ verwendet. Hier sei noch zu erwähnen, dass ebenfalls ein radial basis function (rbf) Kernel getestet wurde. Das Training des Klassifikators war jedoch durch die beschränkte Hardware die uns zur Verfügung stand nicht in absehbarer Zeit durchführbar, weshalb diese Kernelfunktion nicht weiter verfolgt wurde.
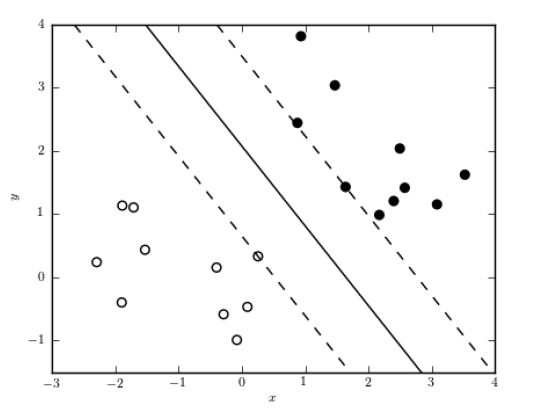
Die gelernten Trenngeraden entscheiden für neue Eingaben, basierend auf den Merkmalen, welcher Klasse die einzelnen Eingaben zuzuordnen sind.
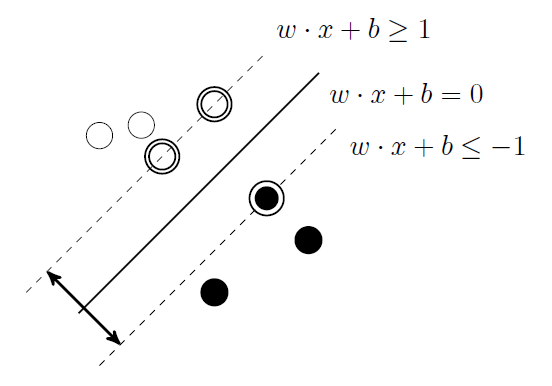
Im vorliegenden Fall versucht der SVC basierend auf den Merkmalen der Bilder in Form eines Vektors $\vec{v} \in \mathbb{R}^{2045}$ eine passende Hyperebene für jede Klasse zu finden. Bedingt durch das verwendetete Package der Bibliothek scikit-learn wird eine “One-vs-Rest”-Strategie verwendet, was bedeutet, dass für jede verfügbare Klasse ein Klassifikator existiert, wobei jeder der Klassifikatoren trainiert wird, um die Klassenbeispiele der eigenen Klasse von den Beispielen aller anderen Klassen (Komplementär-Klassen) zu unterscheiden.
Ergebnisse des Support Vector Classifier
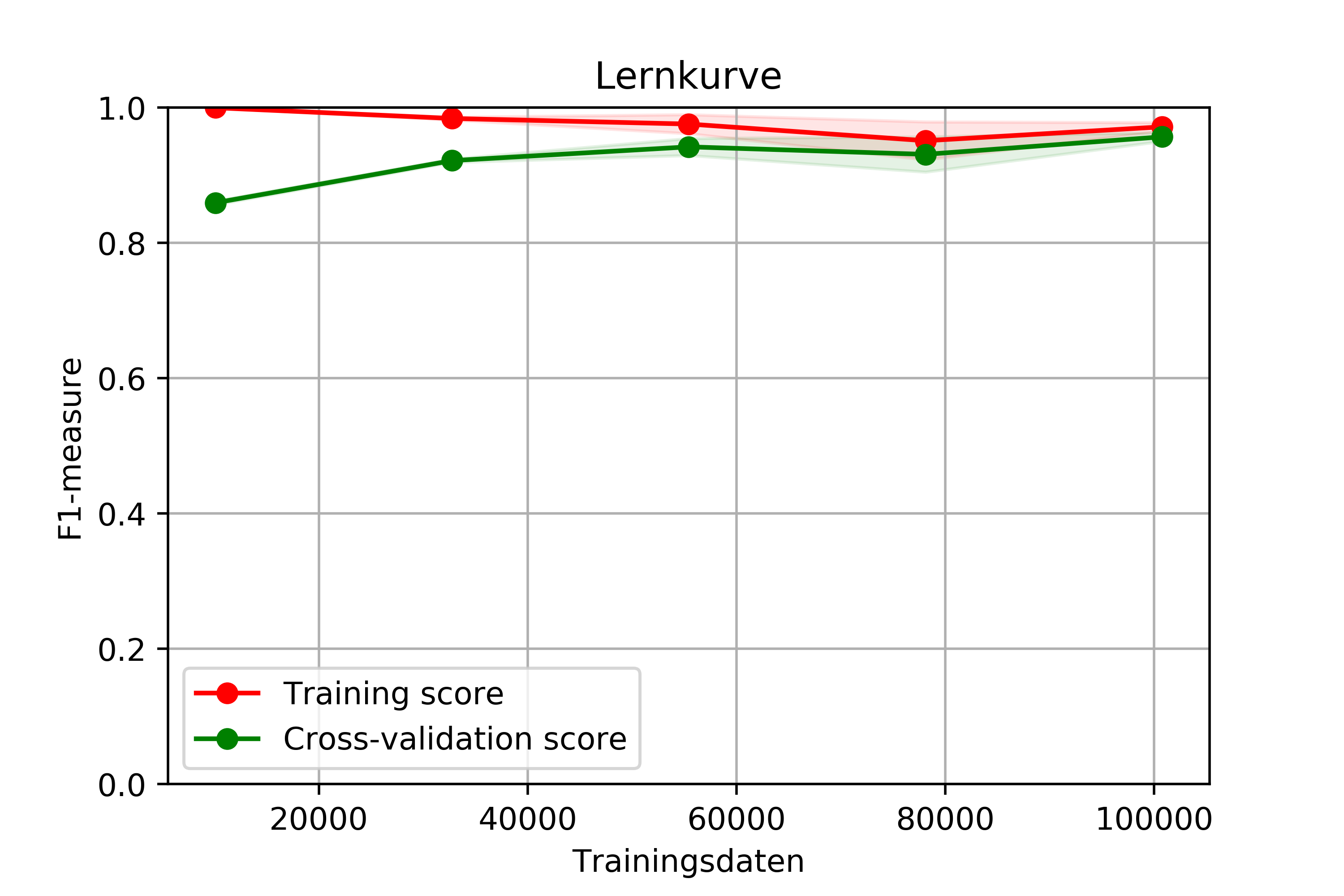
Im Folgenden ist die Lernkurve des SVC dargestellt. Diese zeigt die Metrik des gewichteten F1-Measures (harmonisches Mittel von Precision und Recall)
in Abhängigkeit der Anzahl an Trainingsdaten. Bei Betrachtung der Kurve kann festgestellt werden dass der SVC sehr gute Ergebnisse erzielt und erwartungsgemäß mit steigender Anzahl an Trainingsdaten einen besseren Wert für den F1-Measure erreicht.
Entsprechend können die Ergebnisse des SVC pro Klasse der folgenden Confusion-Matrix entnommen werden.
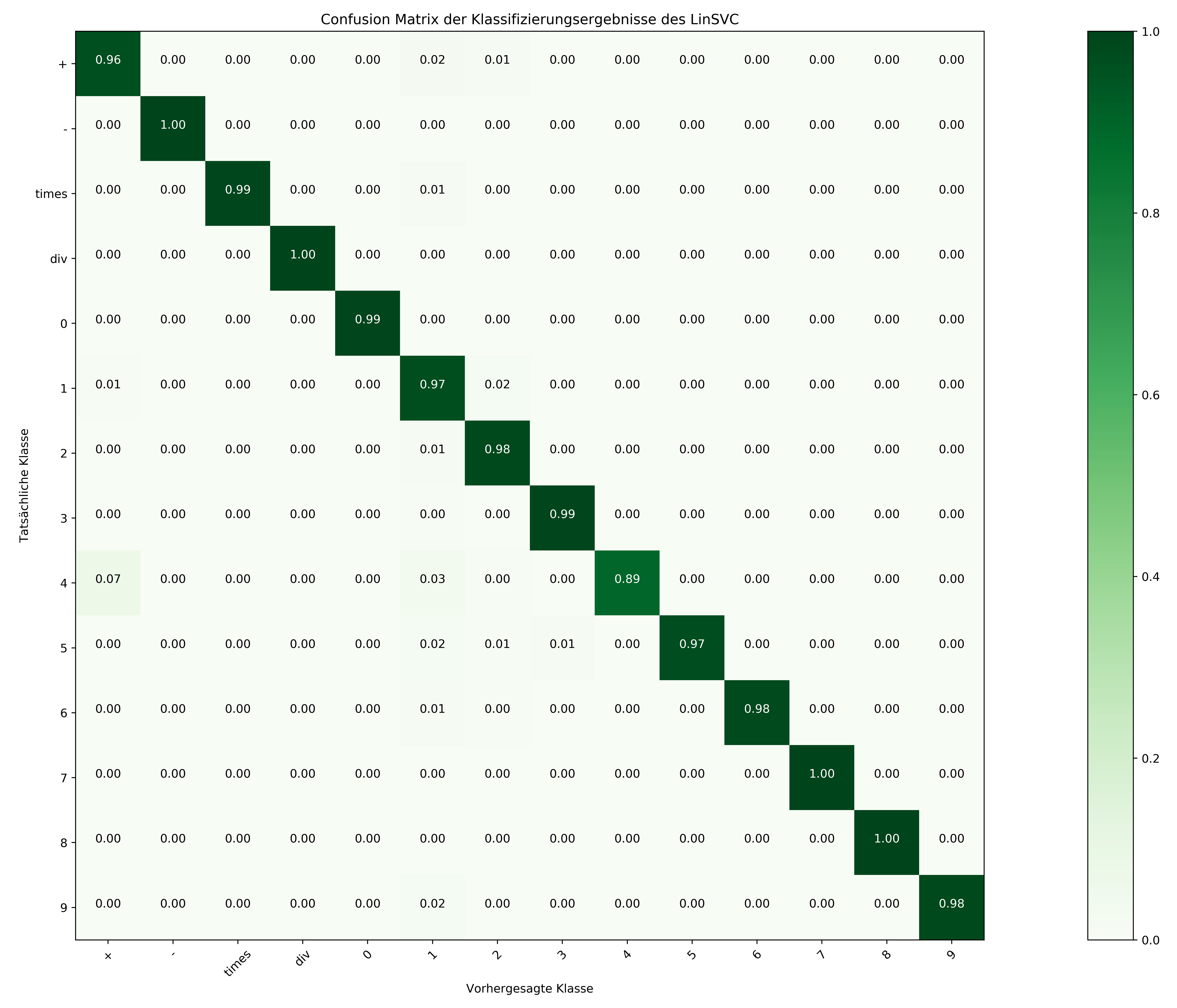
Hier sei noch zu erwähnen, dass die etwas schlechtere Genauigkeit der Klasse $\text{div} (\div)$ womöglich auf die verhältnismäßig geringe Anzahl an Trainingsbeispielen dieser Klasse zurückzuführen ist.
Der Support Vector Classifier lieferte prinzipiell sehr gute Ergebnisse in den Tests und war in der produktiven Applikation zwar besser als die voher betrachteten Algorithmenm jedoch insgesamt noch sehr unsicher und führte zu unverhältnismäßigen, nicht akzeptablen Ergbenissen.
Convolutional Neural Network
Mit dem Einsatz eines Convolutional Neural Networks wurden letztlich die besten Ergebnisse sowohl im Trainings- und Testsprozess als auch in der produktiven Applikation erreicht. Aus diesem Grund wird hier nochmals näher auf den speziellen Aufbau des verwendeten CNN eingegangen. Für die Implementierung des CNN wurde die High-Level Model API Keras basierend auf TensorFlow verwendet.
Spezielles Preprocessing
Da das CNN prinzipiell die Bildmatrix der Beispiele als Eingabe verarbeitet, muss hier wieder der letzte Preprocessing-Schritt rückgängig gemacht werden, sodass die Trainings- und Testdaten wieder ihre ursprüngliche Form einer $45 \times 45$ Matrix besitzen.
Weiter sind die Labels pro Beispiel als “one-hot kodierter” Vektor anzugeben. Im spezifischen Fall entspricht dies einem Vektor $\vec{v} \in \mathbb{R}^{14}$, mit einer “1” an der Stelle, an der die korrekte Klase zu finden ist. Alle anderen Elemente des Vektors sind dementsprechend Nullen.
Das CNN ist bekannt für gute Leistungen im Bereich der Bildverarbeitung. Gerade im Bereich des maschinellen Sehens sind diese Netze durch ihre spezielle Verarbeitungsstruktur den “klassischen” künstlichen Neuronalen Netzten (bsp. Dense-Layer) überlegen und weniger komplex (Feature Extraction und Verarbeitung würde selbst bei kleinen Bildern zu Layern mit mehreren millionen Neuronen führen). Nach verschiedenen Recherchen wurde sich für die folgende Architektur des CNN entschieden:
Architekturkomponenten
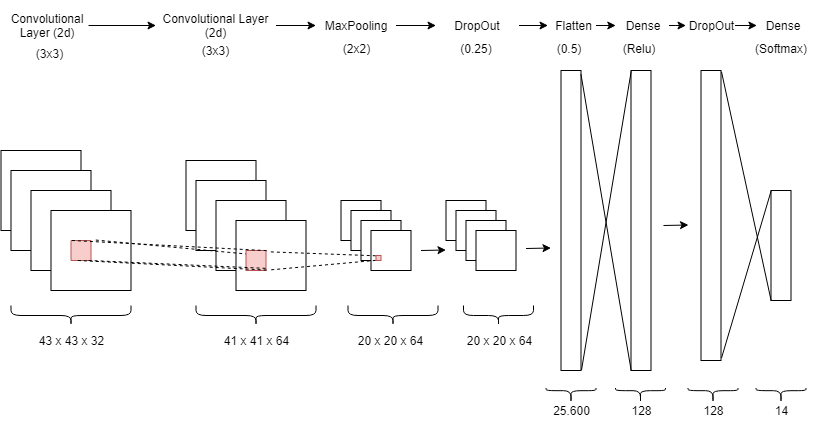
Das Ausgangsbild wird als Bildmatrix $45\times45$ in das CNN übergeben. Der erste Layer ist entsprechend ein Convolutional Layer, der mit einer Anzahl von 32 Filtern das Bild analysiert. Dabei wird eine Filtergröße von $3\times3$ verwendet. Für das Padding wird der Standardwert valid verwendet, sodass kein Padding gesetzt wird. Gleiches gilt für stride (Schrittweite des Filters), hier wurden ebenfalls keine Abweichungen vom Standardwert $1$ angewandt.
Die Output-Größe dieses Convolutional Layers bestimmt werden durch:
$\text{output size} = (\frac{\text{input size} + 2 \times \text{padding} -\text{filter size}}{stride} +1 ) \times (\frac{\text{input size} + 2 \times \text{padding} -\text{filter size}}{stride} +1 )$
Daher beträgt die Output-Größe des ersten Convolutional Layers $43\times 43 \times 32$. Wobei $32$ durch die Anzahl der Filter bedingt ist die im Layer verwendet wurden.
Der zweite Convolutional Layer besitzt eine analoge Spezifikation, sodass Gleiches für die Output-Größe dieses Layers gilt und abhängig durch den Input des vorgeschalteten Layers der Output $41\times41\times64$ beträgt.
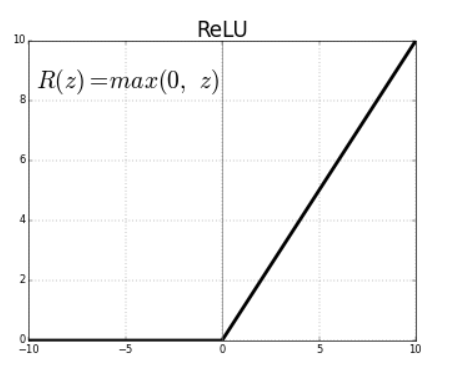
Die Aktivierungsfunktionen für die Neuronen beider Convolutional Layer sind Rectifier. Diese Aktivierungsfunktion sorgt dafür, dass alle Inputwerte über 0 exakt gleich weitergegeben werden, für Inputwerte kleiner 0 wird der Wert 0 weitergegeben.
Im nächsten Schritt wird ein MaxPooling Layer mit einer Größe von $2\times 2$ gewählt, was zu einer Verkleinerung der Matrix im weiteren Verlauf des Netztes führt, in dem für jedes vierte Pixel der maximale Wert als neuen Wert übernommen wird. Das Resultat ist eine Output-Größe von $20\times 20 \times 64$.
Zur Prävention der Überangepasstheit des Modells ist der nächste Schritt ein DropOut, sodass 25% der Neuronen “ausgeschaltet” werden.
Nach den Convolutional Layern ist es notwendig, das Bild in Form einer Matrix in einen Vektor zu überführen (Flatten), sodass dieses als Input für den darauffolgenden Dense Layer benutzt werden kann.
Die $20\times 20\times 64$ Bildmatrix wird so zu einem Vektor $\vec{v} \in \mathbb{R}^{25.600}$.
Der nachstehende Denselayer mit 128 Inputneuronen und der Aktivierungsfunktion Rectifier sorgt für eine Dimensionsreduktion des Vektors $\vec{v} \in \mathbb{R}^{128}$.
Um auch hier wieder das Modell vor der Überangepasstheit zu schützen, wurde ein DropOut Layer verwendet, bevor der Vektor weiter an den letzten Dense Layer übergeben wird.
Dieser nutzt eine Softmax-Funktion und ist für die Berechnung einer Wahrscheinlichkeitsverteilung der eingegebenen Features verantwortlich. Dessen Output-Vektor ist die Wahrscheinlichkeitsverteilung des Input-Bildes über die verfügbaren Klassen.
Dementsprechend ist der Output dieses letzten Layers und des CNN allgemein ein Vektor $\vec{v} \in \mathbb{R}^{14}$, der die Wahrscheinlichkeit dass das Bild zu einer Klasse gehört pro Klasse angibt.
Für das Training des CNN wurde klassischerweise eine Categorical Cross Entropy Kostenfunktion gewählt, die die Leistung eines Klassifikators durch die Abweichungen der Wahrscheinlichkeiten von der tatsächlichen und der vorhergesagten Klasse bestimmt.
Wobei $y_{o,c}$ ein binärer Indikator, ob die tatsächliche Klasse und die vorhergesagte Klasse übereinstimmen. $log(p_{o,c})$ entspricht der Wahrscheinlichkeit, welche für die Klasse $c$ für die Beobachtung $o$ gemacht wurde.
Weiter wurde für die Optimierung das Gradientenverfahren (speziell mit der Lernmethode ADADELTA verwendet). Dieser nutzt zum Aktualisieren der Lernrate eine Begrenzung der Gradienten auf eine feste Fenstergröße und berücksichtigt somit nicht alle vergangenen Gradienten.
Ergebnisse des Convolutional Neural Networks
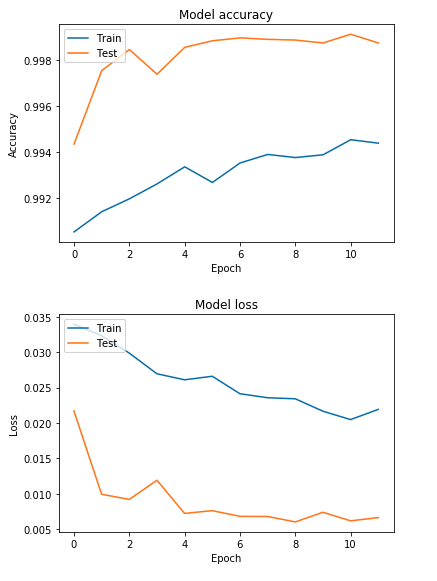
Während des Trainings wurden sehr gute Ergebnisse auf dem Datenset für die Trainings- und Testdaten erzielt. In den beiden nachstehenden Grafiken sind nochmals der Score und parallel die Losses des Trainings über 12 Epochs hin aufgezeigt.
Entsprechend wurde eine sehr gute Klassifikation für die Klassen erreicht, welche der nachfolgenden Confusion Matix zu entnehmen ist.
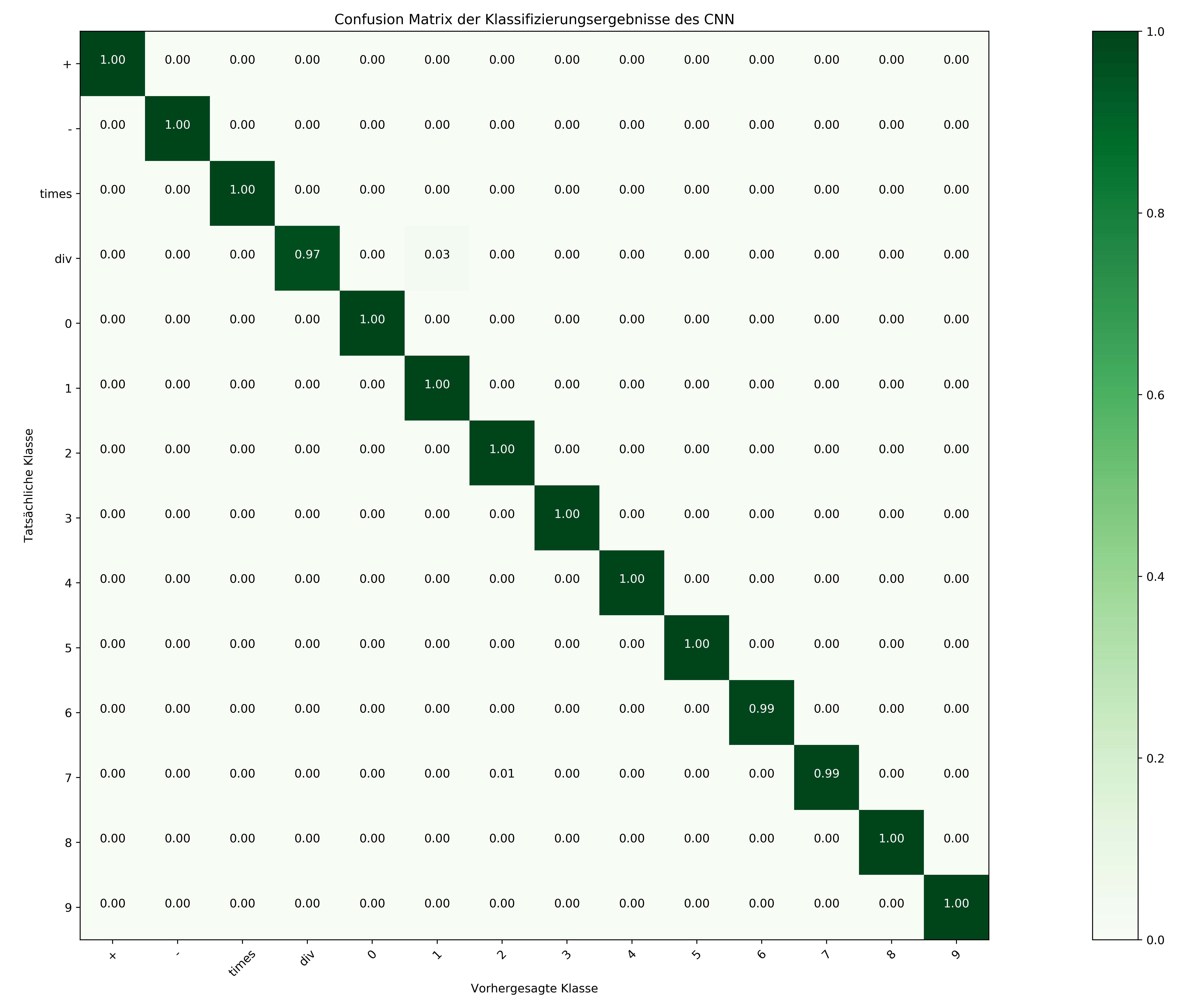
Durch verschiedene Tests in der Applikation erzielte das CNN als Klassifikator für die handschriftlichen Zeichen die besten Ergebnisse.
Applikation
Für die Applikation wurde sich einfachheitshalber ebenfalls für die Programmiersprache Python entschieden. Mithilfe der Bildverarbeitungsbibliothek OpenCV ist es neben der Manipulation von Bildern auch möglich entsprechende Benutzer-Interfaces zu erstellen, auf denen mit der Maus frei gezeichnet werden kann.
In OpenCV werden Bilder als dreidimensionale Arrays mit den Dimensionen [Breite, Höhe, Blau-Grün-Rot-Farbwerte] repräsentiert. Das Zeichenfenster wird nun mit den Werten [1200, 800, (0, 0 ,0)] initialisiert und wird daher von OpenCV als $1200\times800$ Pixel großes, schwarzes Fenster dargestellt.
Wann immer der Nutzer mit gedrückter linker Maustaste auf die leere Fläche zeichnet, werden regelmäßig Positionswerte der Maus an einen Callback übergeben, welcher zwischen den aktuellen und den letzten bekannten Positionswerten eine Linie einzeichnet. Repräsentiert wird diese Linie im Bild durch das Setzen der Farbwerte auf weiß [x, y, (255, 255, 255)] an den relevanten Stellen. Setzt der Nutzer nun ab kann die eigentliche Erkennung erfolgen.
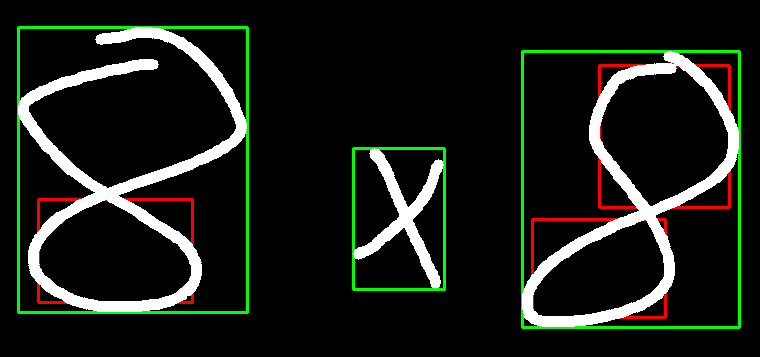
Zunächst müssen die Zahlen und Rechenzeichen voneinander isoliert werden, da das CNN nur einzelne Zeichen verarbeiten kann. Hierzu werden mit OpenCV alle Konturen im gesamten Fenster gefunden und für jede ein Rechteck, das gerade groß genug ist, um die gesamte Kontur zu umranden, bestimmt und eingezeichnet. Aufgrund der Bestimmungsmethode von OpenCV werden hierbei jedoch häufig (speziell für Ziffern, bei denen sich die Striche “kreuzen” wie etwa bei einer 8) pro Zeichen mehrere Konturen gefunden. Um diese zu filtern werden alle Rechtecke betrachtet und für das jeweils größte noch nicht betrachtete Rechteck alle Rechtecke, die komplett innerhalb des größten Rechtecks liegen entfernt. Dies wird solang wiederholt, bis alle Rechtecke entweder bereits betrachtet oder entfernt wurden. Zur Visualisierung werden die kleineren Rechtecke in rot und die größten in grün eingezeichnet. Die grünen Rechtecke markieren die eigentlichen zu verabeitenden Zeichen.
Die Konturen werden im Format (x, y, Breite, Höhe) angegeben. Mithilfe dieser Angaben kann aus dem Array, das die Bildfläche darstellt, der relevante Bereich ausgeschnitten werden. Da die Eingabebilder für das CNN genau 45x45 Pixel groß sein müssen, wird der ausgeschnittene Bereich zunächst so aufgefüllt, dass er quadratisch ist und dann auf 45x45 hoch- bzw. runterskaliert. Des Weiteren müssen die Farbwerte invertiert werden, sodass der Hintergrund weiß (Farbwerte [255, 255, 255]) und das Gezeichnete schwarz (Farbwerte [0, 0 ,0]) ist, was auch der Beschaffenheit der Trainingsdaten geschuldet ist.
Die fertig vorbereiteten Daten werden an das geladene Modell zur Vorhersage übergeben. Das Resultat daraus ist ein 14-dimensionaler one-hot-kodierter Vektor, bei welchem je nach Position des one-hot-codierten Merkmals auf das vorhergesagte Zeichen geschlossen werden kann.
Alle Ergebnisse der Vorhersage können nun einfach auf der Bildfläche dargestellt und aneinandergekettet an die eval() Function übergeben werden, welche entweder einen Fehler für eine unvollständige Rechnung oder ein Ergebnis zum Anzeigen ausgibt.
Ein Beispiel für die Rechnung $10 \times 2 - 1 \div 3$ zeigt folgendes Bild.
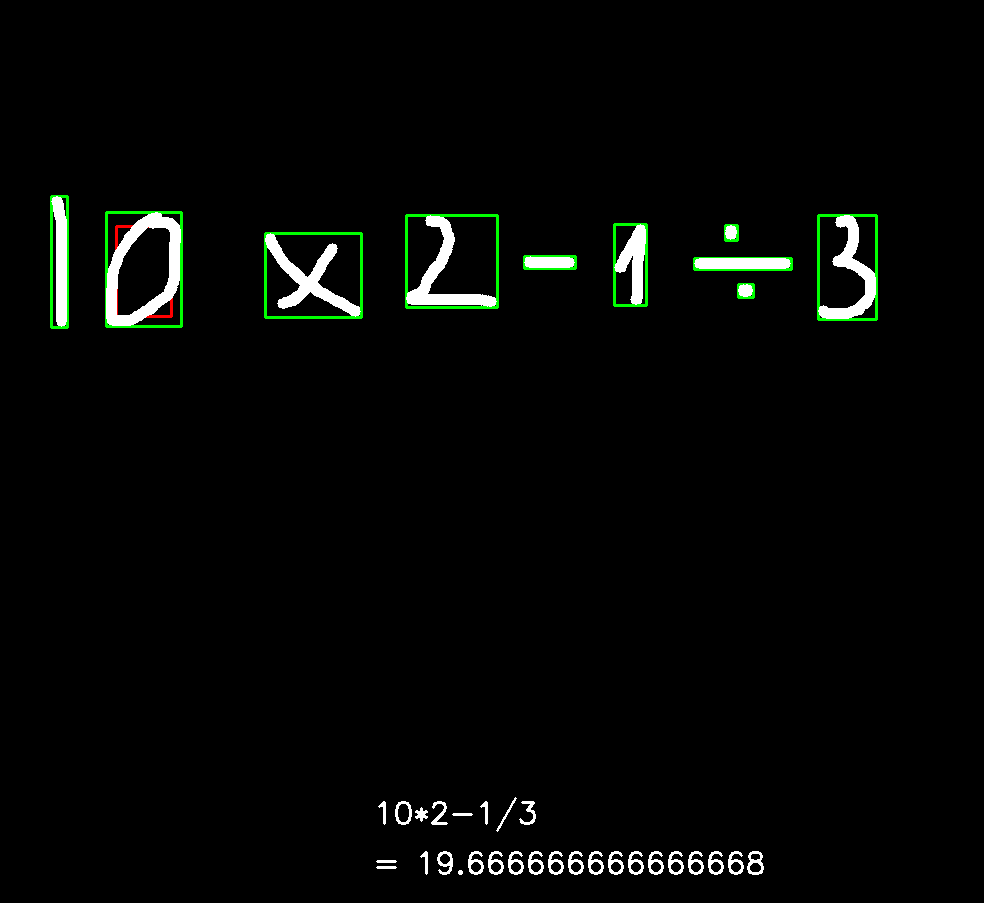
© Tim Anders, Tobias Richstein, Julian Seibel